
PARADOXES
 |
PARADOXES |
Des surfaces à géométrie variable
|
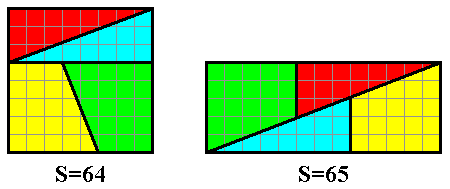
Prenons un carré de 8 sur 8, donc de surface 64. Nous le découpons en 4 comme indiqué sur la figure et nous rassemblons les morceaux différement. Nous obtenons alors un rectangle de 13 sur 5, donc de surface 65. D'où vient cette différence de surface ? |
 |
|
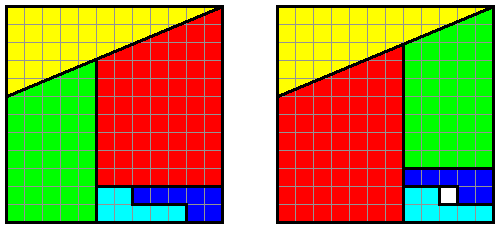
Cette fois, nous partons d'un carré de 12 sur 12, que nous découpons en 5 morceaux. Ces 5 morceaux une fois réassemblés, nous obtenons le même carré de 12 sur 12, mais un trou est apparu. D'où vient-il ? |
 |
|
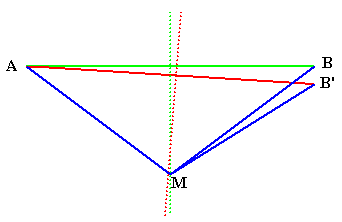
Considérons sur la figure de droite deux points A et B quelconques, et un point B' à même distance de A que B (donc AB=AB'). Nous traçons la médiatrice des segments AB et AB'; ces deux médiatrices se coupent en M. Nous avons donc AM=BM puisque M est sur la médiatrice de AB et AM=B'M puisque M est sur la médiatrice de AB'. Donc, puisque AB=AB', BM=B'M, les deux triangles AMB et AMB' sont identiques; pourquoi ne se superposent-ils pas ? |
 |
|
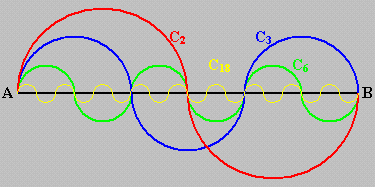
Considérons un segment AB de longueur 1. Nous définissons la courbe Cn de la manière suivante : Nous découpons le segment AB en n sous-segments de longueur 1/n et nous relions les extrémités de ces sous-segments par des arcs de cercle dont ces sous-segments constituent le diamètre, ces arcs de cercle étant orientés alternativement d'un côté et de l'autre du segment AB. La figure de droite montre quelques exemples de courbes Cn. A l'évidence, lorsque n tend vers l'infini, les courbes Cn convergent vers le segment AB. Donc la longueur de ces courbes tend vers la longueur de AB, soit 1. Il est facile de calculer la longueur de Cn : chaque arc de cercle a un diamètre de 1/n, donc la longueur de l'arc de cercle vaut PI/2n; donc, la longueur de la courbe Cn vaut n fois cette valeur, soit PI/2. Donc, PI/2 tend vers 1 lorsque n tend vers l'infini. Où est l'erreur ? |
 |
Une épidémie de flemmingite aigüe frappe la planète.
Un seul médicament, à base d'écorce de bouleau, semble
agir contre cette maladie, mais aucune étude sérieuse n'a encore
été menée; de plus, ce médicament n'est pas encore
produit en quantités suffisantes pour soigner tous les malades.
Au Japon, la maladie ne frappe pas beaucoup, et les médicaments y sont
rares, car peu rentables pour les sociétés pharmaceutiques locales.
Un médecin japonais fait quelques statistiques : il a réussi à
obtenir le médicament pour 10 de ses patients, qui ont tous guéri;
pour 100 autres de ses patients, il n'a rien pu donner, mais 70 d'entre eux
ont fini par guérir quand même.
En France, par contre, la maladie est plus répandue, et quelques lots
du médicament y ont été envoyés en priorité.
Un médecin français fait également des statistiques : il
a réussi à obtenir le médicament pour 100 de ses patients,
dont 50 ont guéri; pour 10 autres patients, il n'a rien pu donner, et
aucun de ces patients non traités n'a guéri.
Ces deux médecins se rencontrent à un congrès et discutent
des résultats indéniables de ce médicament. Les statistiques
sont éloquentes:
|
Taux de guérison avec médicament
|
Taux de guérison sans médicament
|
|
|
Médecin japonais
|
100%
|
70%
|
|
Médecin français
|
50%
|
0%
|
Pour les deux médecins, le médicament a indéniablement favorisé la guérison des patients.
Afin d'avoir plus de poids, ils décident de faire une déclaration commune, et d'agréger leurs statistiques.
Après avoir agrégé leurs statistiques, ils obtiennent les résultats suivants :
Au vu de ces calculs, ils renoncent bien vite à leur déclaration commune. Que s'est-il passé ???